SPSSの使い方 ～IBM SPSS Statistics超入門～ 第9回： SPSSによるクロス集計表 とカイ2乗検定

第9回：２変量の分析（質的×質的）　クロス集計とカイ2乗検定

前回は、量的データ同士の分析である相関分析について解説を加えてきました。今回は、質的データと質的データ同士の関係性を把握するための分析手法、クロス集計表そしてカイ2乗検定について解説をしていきましょう。

２つの量的な変数の関係性を把握するクロス集計とカイ2乗検定

カテゴリーデータ同士の関係性を把握するための手法がクロス集計です。たとえば、お店の満足度調査で、自分のお店の評価を「非常に満足」から「非常に不満」の５段階で調査をしたとしましょう。そこに性別を加え、性別ごとにアンケートの回答に差があるのかを確認してみましょう。これがクロス集計表です。２つの質的変数の関係性を見ることができます。満足度は順序尺度、性別は名義尺度でいずれも質的変数ですね。

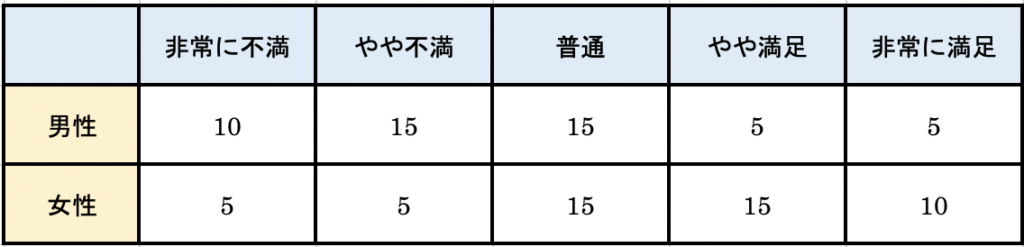
今回のクロス集計を確認すると、どうやら満足度は性別によって差があるように思われます。女性の方が、満足度が高いようにも見えます。しかしながら、本当に差があるとしてもよいのでしょうか？それを確認するために行うのがカイ2乗検定です。カイ2乗検定は、「本来、2つの変数に関係がないのであるとするならば、各セルの度数は人数比に従うはず」
であるというものを帰無仮説にしています。人数比に従うはずであり理論的な値を期待値と言います。
この期待値と実測値の差分の２乗の値を各セルすべて足し合わせたものがカイ２乗値となります。このカイ２乗値がカイ２乗分布のどこ部分かを確認し、帰無仮説の採択するか棄却するかを決定します。それでは、。さっそくSPSSで実行するクロス集計表の作成とカイ2乗検定を実行してみましょう。

SPSSで実行するクロス集計とカイ2乗検定

それでは早速、SPSSでクロス集計を実行していきましょう。

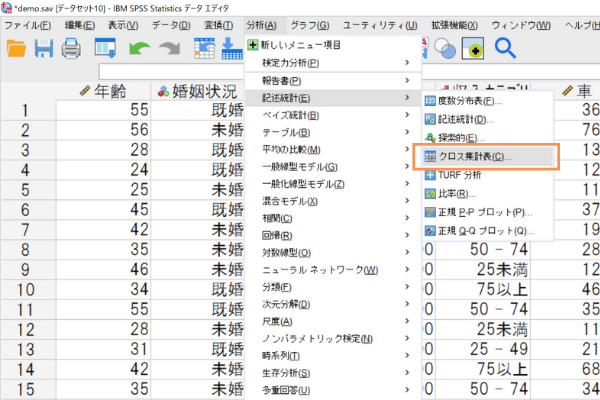
Step1：メニューから「分析」＞「記述統計」＞「クロス集計表」を選択します。

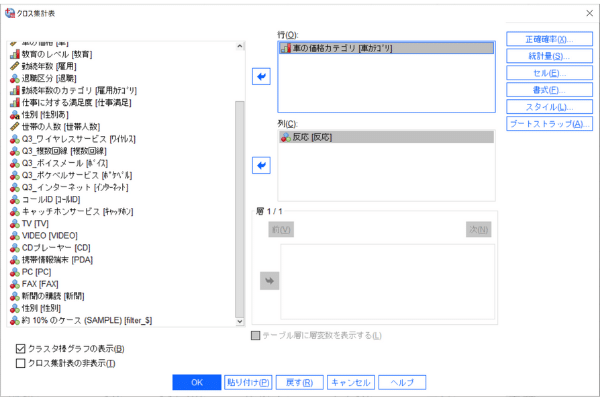
Step2：続いて詳細を設定していきましょう。

前回同様、SPSS Statisticsのデモサンプル、demo.savを利用しています。
今回は、行に「車の価格カテゴリ」を、列に「反応」の変数を選択します。
また、左下の[クラスタ棒グラフの表示]にもチェックを入れましょう。

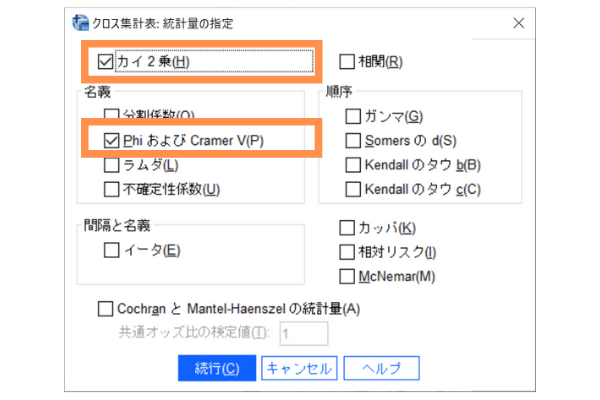
Step 3 : 「統計量」ボタンを押して必要な検定の設定をしましょう。

ここでは、検定を行うための設定を行います。
このダイアログ（画面）では、「カイ2乗」にまずチェックをいれましょう。カイ2乗検定を行う上で必要な設定です。また、効果量を算出するために「PhiおよびCramer V(P)」にチェックをいれます。
設定が終了したら「続行」ボタンを押しましょう。

Step 4 : 続いて「セル」のボタンを押します。

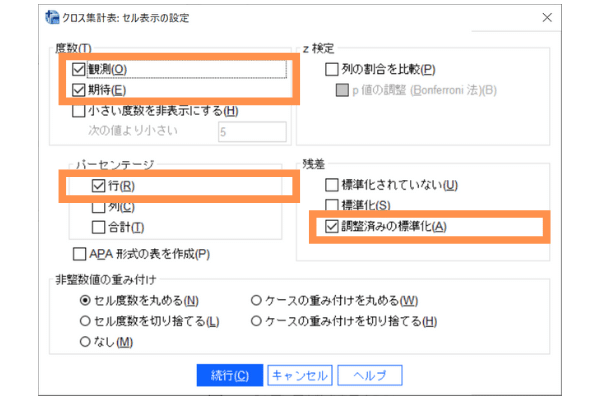
このセルの画面では、「観測」と「期待」にチェックをいれましょう。
また、パーセンテージの[行]にチェックを入れます。さらに「残差」の「調整済みの標準化」にチェックをいれます。チェックを入れ終わったら「続行」 を押します 。
クロス集計表の画面に戻ったら「OK」を押しましょう。

SPSSによるクロス集計・カイ二乗検定の出力の見方

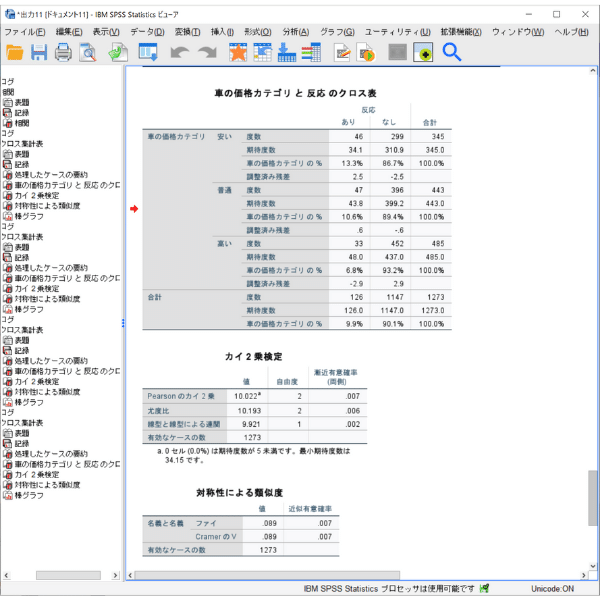
クロス集計表の結果とカイ二乗検定、効果量が出力されます。

まず、一番上にはクロス集計が出力されます。表の中に「期待値」と「観測（実測値）」の値がありますね。「期待値」とは、２つの変数に関係がないする帰無仮説を前提とした上で、各セルに入るべきであろう数のことです。なお、2つの変数（この場合には、車の価格と反応）に関係がない場合には、実測値と期待値が近しい値をとります。逆に関係がある場合には、実測値と期待値の差は開いている状態となります。

たとえば、上の表では、「反応あり」と「車の価格（安い）」のセルを見ていきましょう。期待値は34.1です。観測数（実際の値）は46ですね。この差は12ほどの乖離があります。一方「反応あり」と「車の価格（普通）」セルに注目すれば、期待値は43.8、観測値は47ですね。

この期待値と観測値の乖離度合いを式に当てはめ、計算した結果がカイ2乗値です。カイ二乗検定の欄の「値」はカイ2乗値を示しています。
また、その検定の結果は、「漸近有意確率（両側）」を確認しましょう。

有意水準自体は各研究領域によって異なりますが、５％を有意水準の基準としている場合には、0.05以下の数値であれば有意に差があると判断します。

なお、２×２のクロス表の場合には、Pearsonのカイ２乗検定ではなく、Fisherの直接法の部分を確認します。

IBM SPSS Statistics 29.0.1新機能

統計解析ソフトウェアIBM SPSS Statisticsの最新バージョン「IBM SPSS Statistics 29.0.1」では、データエディタウィンドウにデータの概要表示、生存分析にパラメトリック共有フレイルティモデル、記述統計として指定した特定のパーセンタイルの出力機能が加わりました。

知っておきたいSPSSの使い方：小技Live（無料セミナー）

毎月開催の無料セミナー。SPSS Statisticsのおすすめの機能とその使い方についてデモを交えてご紹介します。

「はじめてのSPSS超入門」オンライントレーニング

統計解析ソフトウェア「IBM SPSS Statistics」をはじめて使い始める方向けのオンライントレーニングコースです。

SPSS 学生版「SPSS Statistics Grad Pack」いつでもどこでも利用可能

SPSSの学生版「IBM SPSS Statistics Grad Pack」は、大学生、大学院生向けに自宅で自身のPCで利用が可能な1年間限定のソフトウェア。当ページでは、便利でお得な学生版についてご紹介。

今回ご紹介ソフトウェア

IBM SPSS Statistics

全世界で28万人以上が利用する統計解析のスタンダードソフトウェアです。1968年に誕生し、50年以上にわたり全世界の統計処理をサポート。データ分析の初心者からプロまでデータの読み込みからデータ加工、分析、出力までをカバーする統合ソフトウェアです。

製品をもっと詳しく知りたい方はこちら