SPSSの使い方 ~ 第10回: SPSSによるt検定〜グループの平均の差を比較する

第10回:グループの平均の差を比較する
SPSSの使い方〜IBM SPSS Statistics超入門〜もいよいよ10回目となりました。
データの読み込みから始まり、基本的な操作を紹介してきましたが、使えるようになりましたでしょうか?
さて、今回は、SPSSによるグループ間の差の検定について解説を進めていきましょう。
二つのグループを比較するという時に、「平均値」を利用して比較する手法、それがt検定です。
さて、グループ間の比較を行う統計手法はいくつか存在します。
詳しくは別のコラムにて解説を行うとして、今回は2つのグループを比較する対応のない2つのグループの差の検定に焦点を当てて解説を行っていきましょう。
対応のない2つのグループの平均値の差の検定
平均値の差の検定は、手元のデータ(標本)において2つのグループの平均値に差があった場合、母集団でも同様の差が見られるのか、統計的にその差が意味のあるものであるのかを確かめる手法です。たとえば、2つのグループの学生に行ったテストの平均点が異なっていた場合、その差が母集団(全体)でも同様に成り立つのか?その2つのグループ間の点数の差には意味があるのか、または偶然なのかを確認するときに利用します。
そのために必要なデータ項目は、グループ(名義)がわかる変数と、平均値を求めるための量的変数です。
なお、2変数より大きい、つまり3つ以上グループを比較するときは、一元配置分散分析などの手法で行います。
さて、それでは2つのグループに差があるかどうかを確かめていきましょう。利用するデータは、これまでと同じサンプルデータ[demo.sav]です。今回は、キャンペーンに反応したグループと反応していない2つのグループによって世帯年収に違いがあるのかを確認していきます。
はじめにグループの比較を見てみよう。
まずはじめに検定を行う前に2つのグループにおいて平均値に差があるのかを基本統計量を利用して確認をしてみることにしましょう。
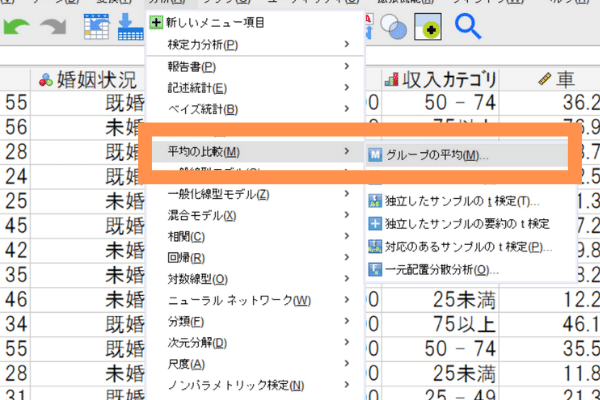
Step1:メニューから[分析]>[平均の比較]>[グループの平均]を選びます。
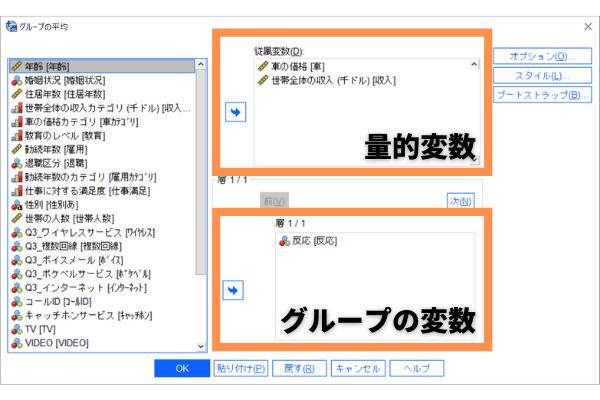
Step2: [グループの平均]ダイアログが表示されます。
ここでは、[従属変数]の部分に量的変数である[世帯全体の収入(千ドル)]を入れます。
さらに[独立変数]部分には、グループを表す変数である[反応]を入れて、「OK」を押します。
ポイントとしては、従属変数部分に量的データ、独立変数にはグループのわかる名義尺度を設定します。なお、今回はt検定ではなくまだグループ間の比較を行うため、独立変数部分は2つ以上のグループがあっても結構です。
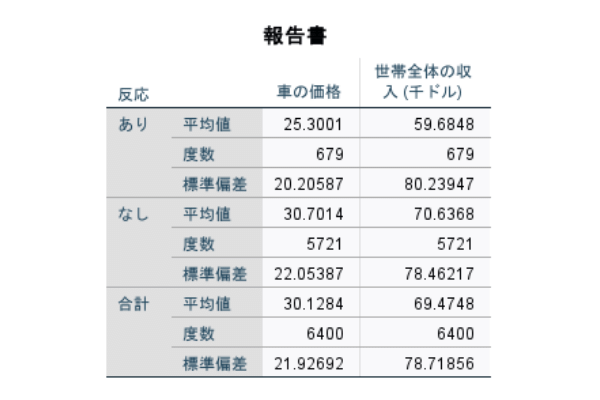
Step3: 出力結果を確認しよう
左のような出力が出てきます。「反応あり」と「なし」で平均値が11(千ドル)ほど違いそうです。平均値を確認すると2つのグループに差があるように見受けられます。統計的に差があるのかを確認する必要があります。そこで今度は、t検定を利用して平均値の差を確かめます。
SPSSによる独立サンプルのt検定の実行
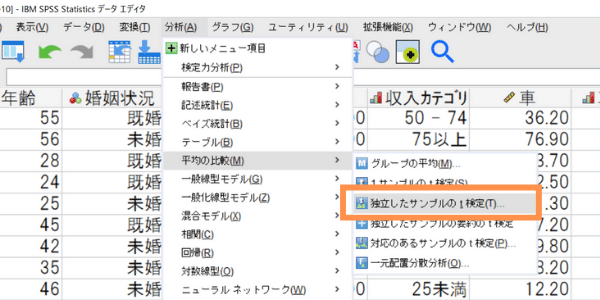
Step1: メニューバーから[分析]>[平均の比較]>[独立したサンプルのt検定]を選びます。
前半部分で紹介したように2つのグループの平均値を比較する際には「独立したサンプルのt検定」を選択します。
Step2: t検定のダイアログの設定
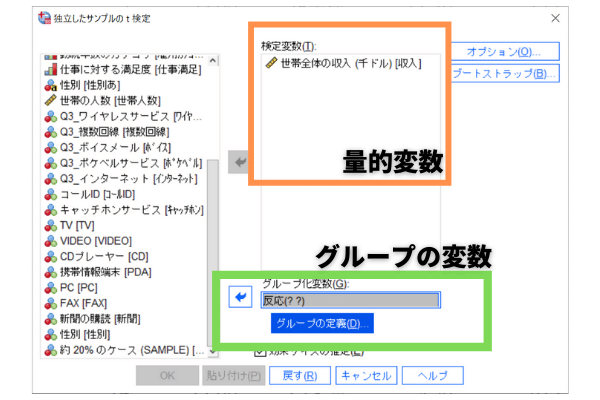
[独立したサンプルのt検定]ダイアログボックスが表示されます。
左側の変数候補リストから確認したい変数である[世帯全体の収入]を選択し、 [検定変数]に入れます。
[グループ化変数]部分には、2つのカテゴリ値をもつ変数を入れます。ここでは[反応]を入れましょう。
「反応(??)となっていますので、「グループの定義」を押して、グループの定義をします。
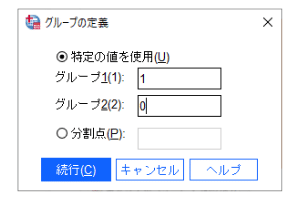
Step3 : グループの定義の設定
この例では、あり=0、なし=1です。そして、「続行」 を押します。
[独立したサンプルのt検定]の画面に戻ると、[グループ化変数]部分が反応(0,1)となっているはずです。これでOKです。
SPSSにおける対応なしの独立サンプルのt検定の出力結果
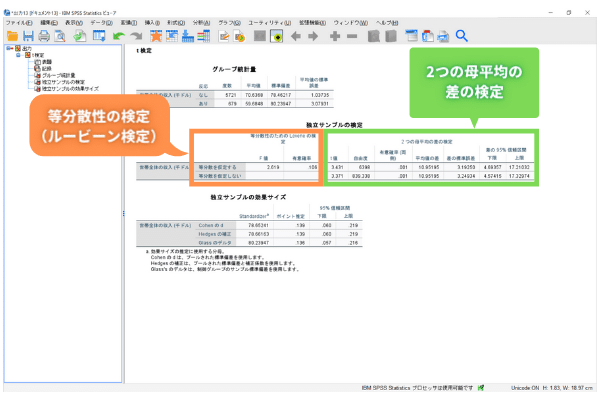
Step4 : t検定の出力を確認しよう
はじめに[グループ統計量]の部分で、各変数の度数や平均値、標準偏差、標準誤差について確認を行います。確認した上で、2つのグループの平均値の差があるかを確認するt検定を行います。
t検定を行う際には、前提条件として以下の3つを満たしていることが求められます。
正規性の検定は事前に行っておいていることが前提となりますが、このt検定では、まず「2つのグループの母集団の分散が等しい」という等分散性の検定を行います。
t検定を行う前提条件
- 標本は無作為に抽出されていること
- 母集団の分散は正規分布もしくはそれに近いものであること
- 2つのグループの母集団の分散が等しいこと

Step 5 : 等分散性のためのLeveneの検定(ルービーン検定)を確認する
SPSSの出力で言えば、[独立サンプルの検定]の左側の部分に該当します。
はじめに[等分散性のためのLeveneの検定]を見てみましょう。この検定においては前述とおり2つのグループの母集団の分散が等分なのかを検定します。この際の帰無仮説は「2つのグループの分散は等しい」、対立仮説は「2つのグループの分散は等しくない」となります。t検定では、「2つのグループの母集団の分散が等しいこと」が前提条件となりますので、帰無仮説を採用したいですね。
通常、検定というと帰無仮説を棄却したい場合が多いのですが、ここは採用をする必要があります。
そのため、この部分の[有意確率]が5%(0.05)を超える場合には、そのまま右側の[2つの母平均の差の検定]に進み、[有意確率(両側)]部分を確認します。今回の結果の場合、[有意確率]が0.106、つまり10.6%です。このため、等分散を仮定していると解釈することができるため[等分散を仮定する]行を確認します。[等分散性のためのLeveneの検定]の有意確率部分が5%に満たない場合には、[等分散を仮定しない]行に進み、右側の[2つの母平均の差の検定]を確認します。
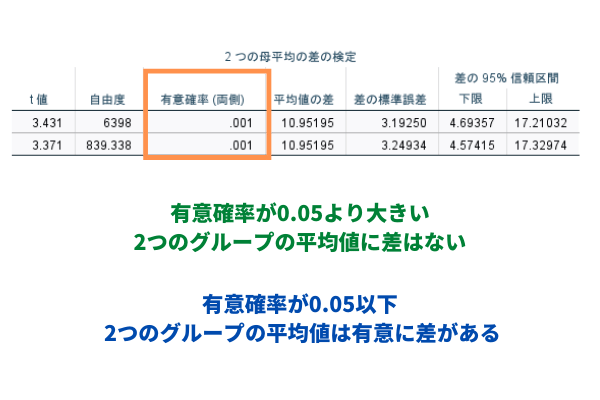
Step 6 : 2つの母平均の差の検定を確認する
右側に移動し、[2つの母平均の差の検定]の[有意確率(両側)]を確認し、0.001となっていますのでその差は母集団においても同様の差があるといえる。統計的に有意であると解釈できます。したがって、ダイレクトメールの反応「あり」「なし」の2つのグループにおいて世帯収入に差があるということがわかります。
平均値の差の検定では、Levene検定の部分の解釈が若干ややこしいとも言えますので、注意をして分析を進めてください。
今回ご紹介ソフトウェア
IBM SPSS Statistics
全世界で28万人以上が利用する統計解析のスタンダードソフトウェアです。1968年に誕生し、50年以上にわたり全世界の統計処理をサポート。データ分析の初心者からプロまでデータの読み込みからデータ加工、分析、出力までをカバーする統合ソフトウェアです。
関連情報
IBM SPSS Statistics 29.0.1新機能
統計解析ソフトウェアIBM SPSS Statisticsの最新バージョン「IBM SPSS Statistics 29.0.1」では、データエディタウィンドウにデータの概要表示、生存分析にパラメトリック共有フレイルティモデル、記述統計として指定した特定のパーセンタイルの出力機能が加わりました。
知っておきたいSPSSの使い方:小技Live(無料セミナー)
毎月開催の無料セミナー。SPSS Statisticsのおすすめの機能とその使い方についてデモを交えてご紹介します。
「はじめてのSPSS超入門」オンライントレーニング
統計解析ソフトウェア「IBM SPSS Statistics」をはじめて使い始める方向けのオンライントレーニングコースです。
SPSS 学生版「SPSS Statistics Grad Pack」いつでもどこでも利用可能
SPSSの学生版「IBM SPSS Statistics Grad Pack」は、大学生、大学院生向けに自宅で自身のPCで利用が可能な1年間限定のソフトウェア。当ページでは、便利でお得な学生版についてご紹介。






