カイ二乗検定における効果量(Cramér’s Vとφ)|SPSSの小技:第6回

クロス集計とカイ二乗検定は、アンケート分析や実務データ分析で非常によく使われます。 ただし、p値(有意・非有意)だけで結論を出すのは危険です。
本記事では、カイ二乗検定における代表的な効果量である Cramér’s V(クラメールのV)と、2×2表で使われる φ(ファイ係数)について、 SPSSでの確認方法と、使い分けのルールを小技として整理します。
よくある誤解
- p値が有意なら「差が大きい」と思ってしまう
- サンプルサイズが大きいと有意になりやすい点を見落とす
- 研究・報告書で「どの程度の関連か」を説明できない
こうした問題を補うのが効果量(関連の強さ)です。
効果量:Cramér’s V と φ(ファイ係数)
カイ二乗検定は「関連があるか(独立ではないか)」を検定します。 一方、効果量は「その関連がどの程度強いか」を示します。
- φ(ファイ係数):2×2のクロス集計(2カテゴリ×2カテゴリ)で用いる効果量
- Cramér’s V:2×2を含む一般のR×C表(2×3、3×4など)で用いる効果量
使い分け(結論)
| クロス集計表 | 推奨する効果量 | 補足 |
|---|---|---|
| 2×2 | φ(ファイ係数) | 2×2ではCramér’s Vと数値が一致します(同値)。 |
| 2×3、3×3、3×4… | Cramér’s V | 一般の分割表に適用でき、比較にも使いやすい指標です。 |
実務上のおすすめ: 2×2なら「φ(ファイ係数)」、それ以外は「Cramér’s V」と覚えるのが安全です。 なお、2×2表では φとCramér’s Vは同じ値になるため、 「Cramér’s Vだけを統一して報告」する運用も可能です(報告書の一貫性重視の場合)。
解釈の目安
| 値(V または φ) | 解釈の目安 |
|---|---|
| 0.10 前後 | 小さい効果 |
| 0.30 前後 | 中程度の効果 |
| 0.50 以上 | 大きい効果 |
※ 上記は一般的な目安です。研究分野や意思決定の文脈により解釈は変わります。
SPSSでの操作手順
Step 1:クロス集計表を開く
メニューから [分析]→[記述統計]→[クロス集計表] を選択します。
メニューからクロス集計表へ
Step 2:行と列に必要な変数を設定します。また、カイ二乗と効果量を設定するために「統計量」をクリックします。
「統計量」ボタンを開き、「カイ二乗」と「PhiおよびCramer V」にチェックを入れます。「続行」ボタンを押し、「OK」を押します。
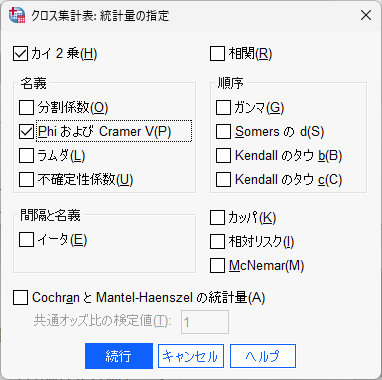
統計量(カイ二乗・効果量)を指定(仮)
Step 3:出力で φ / Cramér’s V を確認する
出力では、まずカイ二乗検定(χ²とp値)を確認し、その後に φ(2×2の場合)またはCramér’s V(一般のR×C表)を確認します。
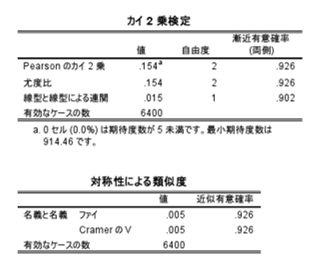
出力(効果量の確認)(仮)
出力結果の読み方(重要)
- p値:関連の有無(統計的に独立かどうか)
- φ / Cramér’s V:関連の強さ(実質的な大きさ)
研究・報告書では「χ²(df), p値, 効果量(φまたはV)」をセットで記載するのが推奨です。
記述例
2×2表の場合: 「カイ二乗検定の結果、有意な関連が認められた(χ²(df)=○○, p=○○)。効果量は φ=0.xx であった。」
一般のR×C表の場合: 「カイ二乗検定の結果、有意な関連が認められた(χ²(df)=○○, p=○○)。効果量は Cramér’s V=0.xx であった。」
よくある注意点
- サンプルサイズが大きいと、弱い関連でもp値が有意になりやすい
- 有意・非有意だけで結論を出さず、効果量も併せて判断する
- 分野の慣習(どの程度で「意味がある」とするか)も考慮する
よくある質問
φ(ファイ係数)とCramér’s Vは何が違うのですか?
φは 2×2表専用の効果量、Cramér’s Vは 一般のR×C表(2×3、3×4など)にも使える効果量です。2×2表では両者は同じ値になります。
2×2表なら、どちらを報告するのがよいですか?
学術的には φ が自然です。一方、レポート全体で統一したい場合は Cramér’s Vに統一しても問題ありません(2×2では同値のため)。
p値が有意なら、効果量は見なくても良いですか?
いいえ。p値は「関連があるか」を示すだけで、「関連の強さ」は分かりません。特にサンプルが大きいと弱い関連でも有意になるため、効果量は必須です。
効果量の目安(小・中・大)はどのくらいですか?
一般的には 0.10(小)、0.30(中)、0.50(大)が目安です。分野や目的によって解釈は変わります。
有意でない場合でも効果量は報告すべきですか?
研究では報告する価値があります。サンプルが小さい場合、効果量が中程度でも有意に届かないことがあります。効果量は解釈の補助になります。


