SPSSによるカイ二乗検定とクロス集計表の作成【第9回｜超入門】p値・効果量・フィッシャー検定・論文の書き方まで完全解説

SPSSによるカイ2乗検定とクロス集計表

前回（第8回）では、量的データ同士の関係性を把握するための「相関分析」について解説しました。今回の第9回では、質的データ（カテゴリーデータ）同士の関係性を分析するための代表的手法である「クロス集計表」と「カイ二乗検定（χ²検定）」を、IBM SPSS Statistics を用いて実践的に解説します。なお、カイ二乗検定、カイ2乗検定、χ²検定などいろんな表記がありますが、すべて一緒です。

今回は、
・クロス集計表とは何か
・カイ二乗検定の理論（期待度数・自由度・p値）
・SPSSによる実行手順
・出力結果の正しい読み方
・2×2表におけるフィッシャーの正確確率検定

までを 研究・実務の両立視点で体系的に解説 します。

クロス集計表とは？SPSSで何ができるのか

クロス集計表とは、2つの質的変数（名義尺度または順序尺度）の組み合わせごとに、度数・割合・分布構造を一覧で可視化する表です。

例えば、

• 性別 × 満足度
• 年代 × 商品購入有無
• 看護介入 × 転帰

といったように、「カテゴリ×カテゴリ」の関係性を視覚的に把握できます。
カテゴリーデータ同士の関係性を把握するための手法がクロス集計です。たとえば、お店の満足度調査で、自分のお店の評価を「非常に満足」から「非常に不満」の５段階で調査をしたとしましょう。そこに性別を加え、性別ごとにアンケートの回答に差があるのかを確認してみましょう。これがクロス集計表です。２つの質的変数の関係性を見ることができます。満足度は順序尺度、性別は名義尺度でいずれも質的変数ですね。

今回のクロス集計を確認すると、どうやら満足度は性別によって差があるように思われます。女性の方が、満足度が高いようにも見えます。

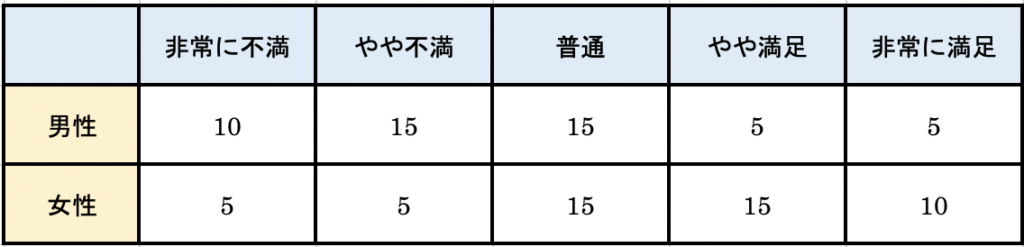
ただし、クロス集計表だけでは
「見た目の差が本当に統計的に意味のある差なのか？」
は、判断できません。そこで用いるのがカイ二乗検定（χ²検定）です。

SPSSでクロス集計とカイ二乗検定を実行する方法

ここからは IBM SPSS Statistics を用いて、実際にクロス集計とカイ二乗検定を実行していきます。サンプルデータには SPSS 標準搭載の demo.sav を使用します。

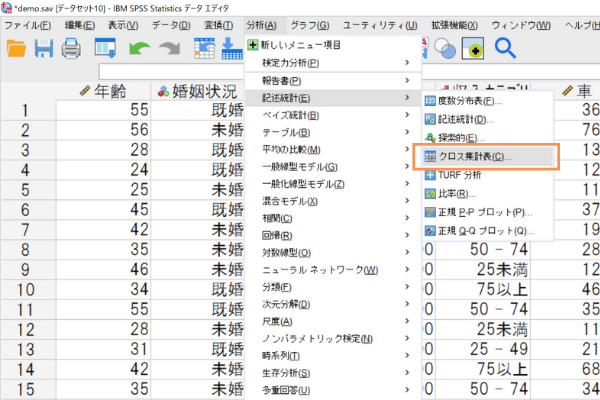
Step1：メニューから「分析」＞「記述統計」＞「クロス集計表」を選択します。

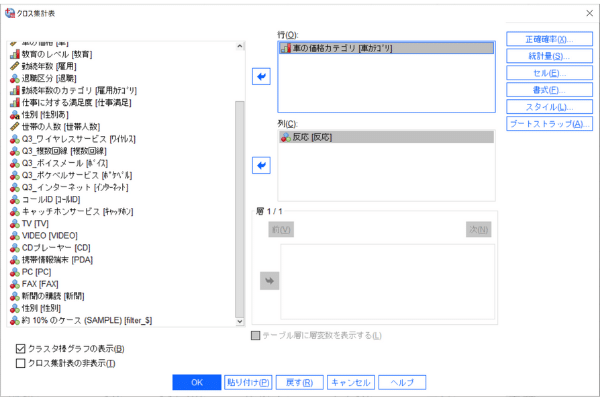
Step2：続いて詳細を設定していきましょう。

前回同様、SPSS Statisticsのデモサンプル、demo.savを利用しています。
今回は、行に「車の価格カテゴリ」を、列に「反応」の変数を選択します。
また、［クラスタ棒グラフの表示］ にチェックを入れることで、視覚的な分布も確認できるようになります。

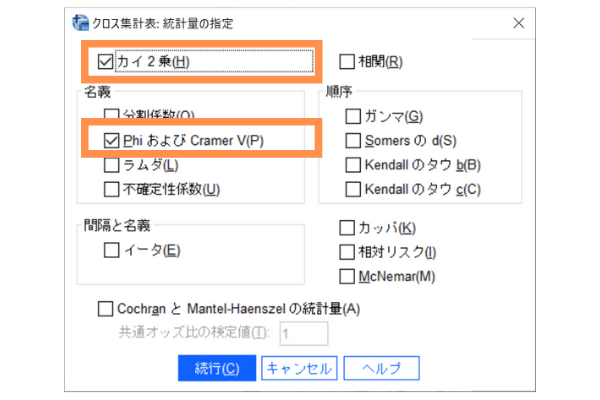
Step 3 : 「統計量」ボタンを押して必要な検定の設定をしましょう。

ここでは、検定を行うための設定を行います。
[統計量]ボタンをクリックし、以下にチェックを入れます。
・「カイ2乗」
・「PhiおよびCramer V(P)」（効果量）
これにより、
・ｐ値による有意差検定
・所属関係の強さ（効果量）
の両方を同時に評価することができます。
設定が終了したら「続行」ボタンを押しましょう。

Step 4 : 続いて「セル」のボタンを押します。

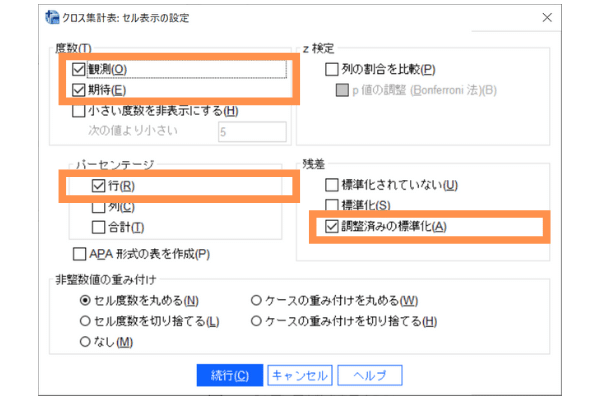
このセルの画面では、「観測」と「期待」にチェックをいれましょう。
また、パーセンテージの[行]にチェックを入れます。さらに「残差」の「調整済みの標準化」にチェックをいれます。チェックを入れ終わったら「続行」 を押します 。
クロス集計表の画面に戻ったら「OK」を押しましょう。

SPSSによるクロス集計・カイ二乗検定の出力結果の見方
（p値・期待値・残差・効果量まで完全解説）

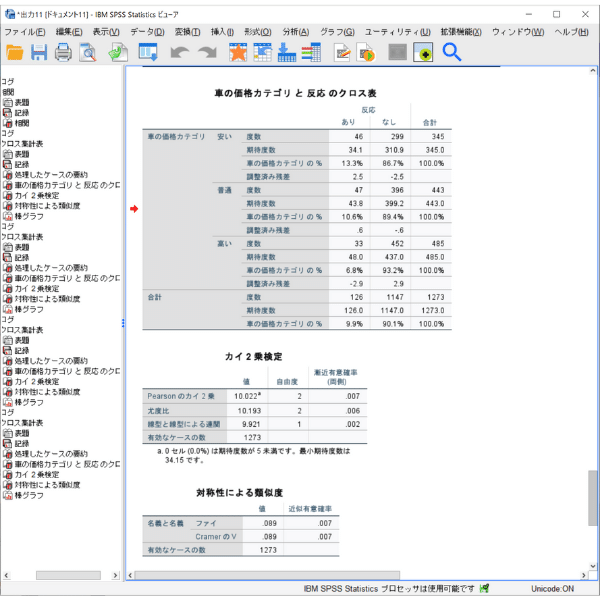
SPSSでクロス集計およびカイ二乗検定を実行すると、主に以下の4種類の情報が出力されます。これらは順番に見ることで、統計的に一貫した解釈が可能になります。

1. クロス集計表（観測値・期待値・割合）
2. カイ二乗検定の検定結果（χ²値・自由度・p値）
3. 効果量（Phi係数・Cramer’s V）
4. 調整済み標準化残差

クロス集計表（観測値と期待値）

まず、一番上にはクロス集計表が出力されます。表の中に「期待値」と「観測（実測値）」の値がありますね。「期待値」とは、２つの変数に関係がないする帰無仮説を前提とした上で、各セルに入るべきであろう数のことです。「観測値」は実際のデータでの度数です。なお、2つの変数（この場合には、車の価格と反応）に関係がない場合には、実測値と期待値が近しい値をとります。逆に関係がある場合には、実測値と期待値の差は開いている状態となります。

ちなみに期待値は、次のように計算できます。

期待値 ＝（行の合計 × 列の合計）÷ 全体の合計

ここでの重要ポイント
・観測値 ≒ 期待値（観測値と期待値の値が近い場合）： ほぼ関係がない可能性が高い
・観測値と期待値の乖離が大きい ：関係がある可能性が高い

クロス集計表はあくまで
「関係がありそうかどうかの“視覚的仮説生成”の段階」です。
最終判断は次の カイ二乗検定のp値で行います。
 

カイ二乗検定の検定結果（χ²値・自由度・p値）

次に表示されるのが 「カイ二乗検定」テーブルです。ここで必ず確認するのは次の3項目です。

・カイ二乗値（χ²）：観測値と期待値のズレの大きさ
・自由度（df）：（行−1）×（列−1）
・漸近有意確率（p値）：差が“偶然かどうか”の確率

この期待値と観測値の乖離度合いを式に当てはめ、計算した結果がカイ2乗値です。カイ二乗検定の欄の「値」はカイ2乗値を示しています。また、その検定の結果は、「漸近有意確率（両側）」を確認しましょう。

有意性の判断基準

有意水準自体は各研究領域によって異なりますが、５％を有意水準の基準としている場合には、0.05以下の数値であれば有意に差があると判断します。

・p < 0.05 → 統計的に有意な差がある
・p ≥ 0.05 → 有意差なし（偶然の範囲）

例えば、
・p = 0.032 → 有意差あり
・p = 0.247 → 有意差なし

と判断します。

2×2表の場合は「フィッシャーの正確確率検定」を優先

　クロス表が 2×2のとき（例：男女×有無）で、期待度数が5未満のセルが存在する場合には、Pearsonのカイ二乗検定は使えません。その場合は必ず「Fisherの直接法（フィッシャーの正確確率検定）」のp値を確認します。SPSSでは自動でPearsonのカイ二乗検定とフィッシャーの正確確率検定が 同時に出力されるため、2×2表では Fisher を最優先で解釈するのが研究倫理上も正解です。

効果量（Phi係数・Cramer’s V）の見方

　p値は「差があるかどうか」は分かりますが、「どれくらい強い関係か」までは分かりません。そこで用いるのが 効果量です。

・Phi係数　：　2×2のクロス集計表
・Cramer's V　：　2×2以外のクロス集計表

Cramer’s V の目安（社会科学・医療系共通）
・0.1未満：ほぼ関係なし
・0.1〜0.3：弱い関係
・0.3〜0.5：中程度の関係
・0.5以上：強い関係

こちらは学問領域によって異なりますので先行研究などを確認しましょう。

調整済み標準化残差
（どのセルが有意差の原因か）

　調整済み標準化残差は、「どのセルが有意差の原因になっているか」を特定するための指標です。

残差の絶対値 解釈
・1.96以上 5%水準で有意
・2.58以上 1%水準で有意

これにより、どのカテゴリ同士が“特にズレているのか”どこが差の本質なのかを 数値で説明可能になります。

論文等の報告の仕方について

　今回の場合には、「性別と満足度の間には有意な関連が認められた（χ²(4)=12.84, p<.05, Cramer’s V=0.31）。特に女性×高満足度のセルにおいて調整済み残差が有意に高かった。」というように表記しましょう。

よくある質問（SPSSのカイ二乗検定・クロス集計）

SPSS Statistics 31.0.1 新機能をご紹介

最新バージョンSPSS Statistics 31.0.1の新機能をご紹介。AI出力アシスタント、Borutaの変数選択、t検定に関するキュレーションヘルプなど様々な機能が追加されました。

知っておきたいSPSSの使い方：小技Live（無料セミナー）

毎月開催の無料セミナー。SPSS Statisticsのおすすめの機能とその使い方についてデモを交えてご紹介します。

「はじめてのSPSS超入門」オンデマンドトレーニング

統計解析ソフトウェア「IBM SPSS Statistics」をはじめて使い始める方向けのオンデマンドトレーニングコースです。

SPSS 学生版「SPSS Statistics Grad Pack」いつでもどこでも利用可能

SPSSの学生版「IBM SPSS Statistics Grad Pack」は、大学生、大学院生向けに自宅で自身のPCで利用が可能な1年間限定のソフトウェア。当ページでは、便利でお得な学生版についてご紹介。

今回ご紹介ソフトウェア

IBM SPSS Statistics

全世界で28万人以上が利用する統計解析のスタンダードソフトウェアです。1968年に誕生し、50年以上にわたり全世界の統計処理をサポート。データ分析の初心者からプロまでデータの読み込みからデータ加工、分析、出力までをカバーする統合ソフトウェアです。

製品をもっと詳しく知りたい方はこちら