SPSS Statistics 30 新機能をご紹介

統計解析のスタンダードツールとして、全世界、国内でも非常に多くのユーザーが利用する「IBM SPSS Statistics」の最新バージョン「IBM SPSS Statistics 30」がリリースされました。最新バージョン「IBM SPSS Statistics 30」ではブランド・アルトマン分析や多変量正規性検定、単変量正規性検定などの最新の回帰分析機能が追加されたほか、ダークモードやフォント機能の強化、チャート機能の強化など大幅な機能拡張が行われています。

【新機能１】
ブランド・アルトマン分析
～Bland Altman Analysis～

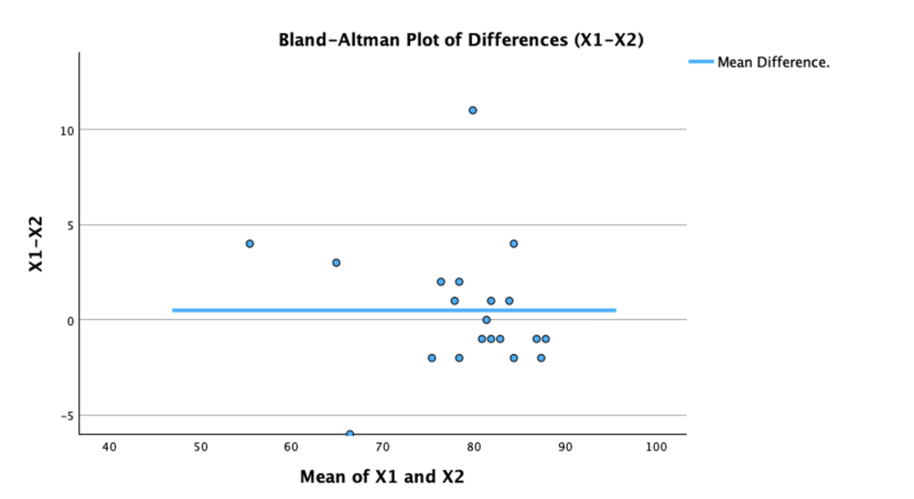
　Bland Altman Analysis（ブランド・アルトマン分析）は、2つの異なる測定方法の一致度をグラフで評価する手法です。
　結果のグラフは散布図XYの軸表現され、Y軸は2つの対応のある測定値(A-B)の差を示し、X軸はこれらの測定値の平均((A+B)/2)を表します。つまり、2 つの対応のある測定値の差は、2 つの測定値の平均に対してプロットされます。
　ばらつきがゼロに近いほど、2つの測定方法は一致しているといえます。信頼区間(±1.96×SD)が狭いほど、測定誤差が小さいことを示し、2つの測定方法は一致している可能性が高いと解釈されます。

【新機能２】
正規性の検定とプロット

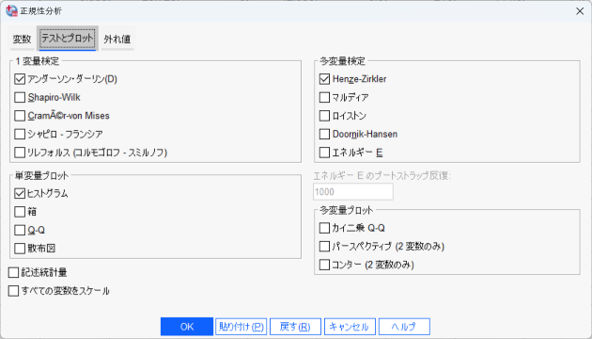
これまでの分析メニュー＞記述統計＞探索的の作図から選択できた正規性の検定とプロットのシャピロ・ウィルクやリレフォルス(コルモゴロフ・スミルノフ)の検定に加えて、新たに追加された正規性分析のメニューからアンダーソン・ダーリングをはじめとした多くの1変量・多変量の正規性の検定やプロット機能が選択できるようになりました。
詳しくはこちら

【新機能3】

ダークモード機能

アプリの背景を暗い色に切り替え、デバイス画面から発せられる光を軽減するデザイン機能を導入しました。
特に低照度の環境では、ダークモードは目に優しく、まぶしさを最小限に抑え、長時間の使用でも快適です。

【詳しく解説】正規性の検定とプロット

　正規性の検定は、データが正規分布に従っているかどうかを確認するために行われる統計的手法です。多くの統計手法(たとえば、t検定や分散分析など)は、データが正規分布に従うことを前提としているため、事前にその前提条件が満たされているかどうかを確認することが重要です。

1変量の正規性の検定

検定名	概要	使用条件	特徴
アンダーソン・ダーリング検定 Anderson-Darling Test	データが特定の分布に従うかどうかを調べる検定で、特に正規分布を評価するために使用する、累積分布関数をベースにした手法。	データ数が少なくても比較的信頼できる結果を得やすい。比較的敏感な検定。	尾部の偏差に敏感で、分布の尾に異常がある場合に有効。
シャピロ・ウィルク検定 Shapiro-Wilk Test	正規分布の仮定のもとで、サンプルの分布が正規分布に従うかを評価するための最も一般的な検定の1つ。	データ数が3~5000の範囲で推奨されるが、小さなサンプルでも有効。	正規性の検定としては非常に強力で、少数のデータセットでも正確に動作。
クラメール・フォン・ミーゼス検定 Cramer-von Mises Test	累積分布関数を使用して、観測データが正規分布に従うかどうかを判断する検定。	データ数が少ない場合でも有効。	全体的な分布の偏差に敏感で、アンダーソン・ダーリング検定よりも幅広く分布全体を評価。
シャピロ・フランシア検定 Shapiro-Francia Test	シャピロ・ウィルク検定のバリエーションで、特に対数正規分布を仮定する場合に効果的。	データ数が多い場合や、対数正規分布の検定に適用されることが多い。	シャピロ・ウィルク検定に似ているが、特に対数正規分布に強く適している。
リレフォルス検定 Lilliefors(Kolmogorov-Smirnov)Test	コルモゴロフ・スミルノフ検定としても知られる方法で、累積分布関数に基づいてデータが正規分布に従うかどうかを評価。	サンプルサイズが比較的大きい場合に適しているが、検出力が他の検定より低い。	比較的大きなデータセットに有効ですが、他の手法に比べると敏感ではないため、検出力が低い。多くの分布に適用可能だが、データ範囲の特異性に敏感。

多変量の正規性の検定

検定名	概要	使用条件	特徴
ヘンツェ・ジルクラー検定 Henze-Zirkler Test	エネルギー距離に基づいた正規性検定で、多変量の正規性を評価する。標本の平均と共分散に依存しないため、一般的にロバスト。	特にサンプルサイズが小さくても使用可能。	非常に汎用的で、サンプルサイズが少なくても高いパフォーマンスを発揮。高次元データに対しても適用可能。
マルディア検定 Mardia Test	多変量の歪度と尖度を用いて正規性を評価する手法。特に歪度や尖度に偏りがある場合に敏感。	比較的大きなサンプルサイズを前提としている。	歪度と尖度を検定することで正規性を判定。大きなデータセットに向いているが、データが高次元になると検出力が低下することがある。
ロイストン検定 Royston Teat	シャピロ・ウィルク検定をベースにした多変量バージョンで、個別の変数ごとの正規性をまず評価し、その結果を組み合わせて多変量正規性を判断する。	各変数が少なくとも3つ以上のサンプルを持つ必要がある。	各変数のシャピロ・ウィルク検定の結果を組み合わせて全体の正規性を評価するため、データの偏差を正確に検出可能。比較的小さなデータに向いている。
ドアネイル・ハンセン検定 Doornik-Hansen Test	多変量の正規性に基づいた尤度比検定法で、線形変換のもとでの正規性を評価する。	正規性を仮定し、線形変換されたデータに基づく検定。	正規分布のデータに強いが、複雑なデータには弱い。データが正規分布に極めて近い場合に有効。検出力は高いが、ノイズに対して敏感。
エネルギー検定 Energy Distance Test	多変量エネルギー統計量を使用した正規性検定で、データのエネルギー距離を基準にして正規性を評価する。	高次元のデータに対しても適用可能。	高次元データに対して有効であり、正規性からの逸脱を高い精度で検出できる。標本サイズや次元の増加に強いが、計算コストが高い。

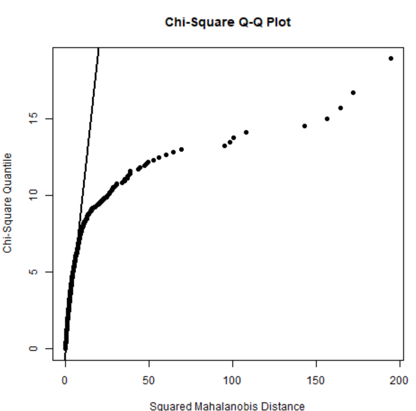
カイ二乗Q-Qプロット

　Q-Qプロット（Quantile-Quantile Plot）は、データセットがある確率分布に従うかどうか、またはデータの2つのサンプルが同じ母集団から得られたかどうかを決定するためのグラフ手法です。カイ二乗として分布すべきデータ・ベースの値と、カイ二乗分布からの対応する分位数との関係を示します。

パースペクティブプロットとコンタープロット

　パースペクティブプロットは、データがどこで収集され、2つの変数がどのように互いに相関しているかについての情報を与えます。これは3次元で構成され、2次元は2つの変数の値、3次元は1変量の場合と同様、多変量正規確率密度関数の値である。
　コンター（等高線）プロットと、透視プロットの2次元空間への射影を含み、これは多変量正規性の仮定をチェックするために使用できます。2変量正規分布データでは、透視図から3次元のベル型グラフが得られ、等高線プロットでも同様のパターンが観察できます。

そのほかのSPSS Statistics 30 新機能

ツールバーの更新

ツールバーにデフォルトで表示されるツールにデータエディタ、出力ビューア、シンタックスの各ウィンドウに切り替えるアイコンが追加されました。

フォントのズーム

Windows ユーザーがグラフだけでなくアプリケーション全体でフォントをズームできる機能が導入され、メニュー、ダイアログボックス、ヘッダー、その他フォントが使用されているあらゆる場所に適用されます。

ライセンス情報を提示

起動画面、ステータスバー、ライセンス管理画面では、試用期間終了までの残り日数が表示されます。タイトルバーには、ユーザーが現在トライアルモードであるかどうかも表示されます。

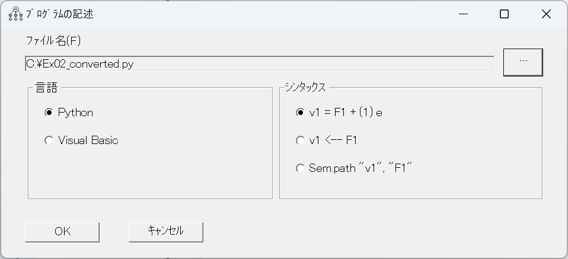
Amos30.0の新機能

Python プログラミングのサポートを提供します。examplesフォルダには、ユーザーズガイドの例の Python プログラムが含まれています。「プログラムの書き込み」ダイアログに、パス図で指定されたモデルに適合する Python プログラムを生成するためのオプションが含まれるようになりました。

【新機能１】
ブランド・アルトマン分析
～Bland Altman Analysis～

【新機能２】
正規性の検定とプロット

【新機能3】

ダークモード機能